5 Spatial log-Gaussian Cox process
A log-Gaussian Cox Process (LGCP) is a doubly stochastic spatial point process. In the simplest case, the intensity of the point process over space is given by \[\Lambda(s) = \text{exp}(\beta_0 + G(s) + \epsilon)\] where \(\beta_0\) is a constant, known as the intercept, \(G(s)\) is a Gaussian Markov Random Field (GMRF) and \(\epsilon\) an error term.
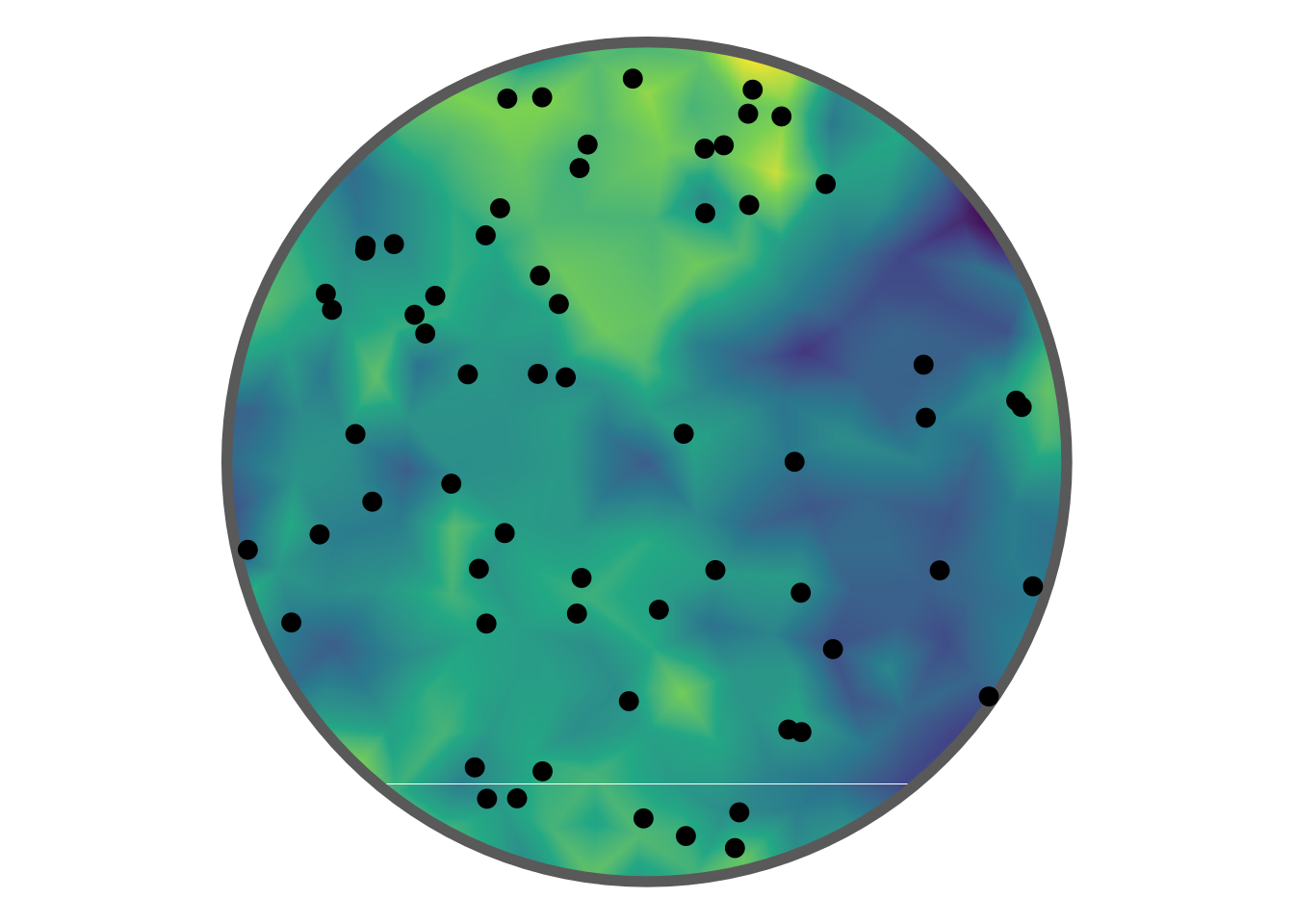
Plotted below is a realisation of a LGCP within a disc shaped region overlain on the latent GMRF.
Following the Stochastic Partial Differential Equation (SPDE) approach proposed by Lindgren, Rue, and Lindström (2011) a Matérn covariance function is assumed for \(G(s)\):
\[C(r; \sigma, \kappa) = \frac{\sigma^2}{2^{\nu-1} \Gamma(\nu)} (\kappa \:r)^\nu K_\nu(\kappa \: r)\]
where \(\kappa\) is a scaling parameter and \(\sigma^2\) is the marginal variance (\(\nu\) is typically fixed, see Lindgren, Rue, and Lindström (2011)). Rather than the scaling parameter, a range parameter \(r=\frac{\sqrt{8}}{\kappa}\) is typically interpreted (corresponding to correlations near 0.1 at the distance \(r\)). The standard deviation is given as \(\sigma=\frac{1}{\sqrt{4\pi\kappa^2\tau^2}}\). In the figure above \(\beta = 3\), \(\text{log}(\tau) = 1.6\), and \(\text{log}(\kappa) = 1.95\).
5.1 Delauney triangluations when fitting LGCP models
TODO
5.2 Fitting a LGCP model
Using spatstat to simulate a LGCP
win <- spatstat.geom::disc()
## here mu is beta0
set.seed(1234)
sim <- spatstat.random::rLGCP("matern", mu = 3,
var = 0.5, scale = 0.7, nu = 1,
win = win)## plotting the simulated (log) random field using ggplot
xs = attr(sim, "Lambda")$xcol; ys = attr(sim, "Lambda")$yrow
pxl <- expand.grid(x = xs, y = ys)
pxl$rf <- as.vector(attr(sim, "Lambda")$v) |> log() - 3 ## minus the intercept
require(ggplot2)
ggplot() +
geom_tile(data = pxl, aes(x = x, y = y, fill = rf), ) +
labs(fill = "") + xlab("") + ylab("") +
scale_fill_viridis_c(option = "D", na.value = NA) +
coord_equal() + theme_void() +
geom_sf(data = sf::st_as_sf(win), fill = NA, linewidth = 2) +
geom_point(data = data.frame(x = sim$x, y = sim$y), aes(x = x, y = y))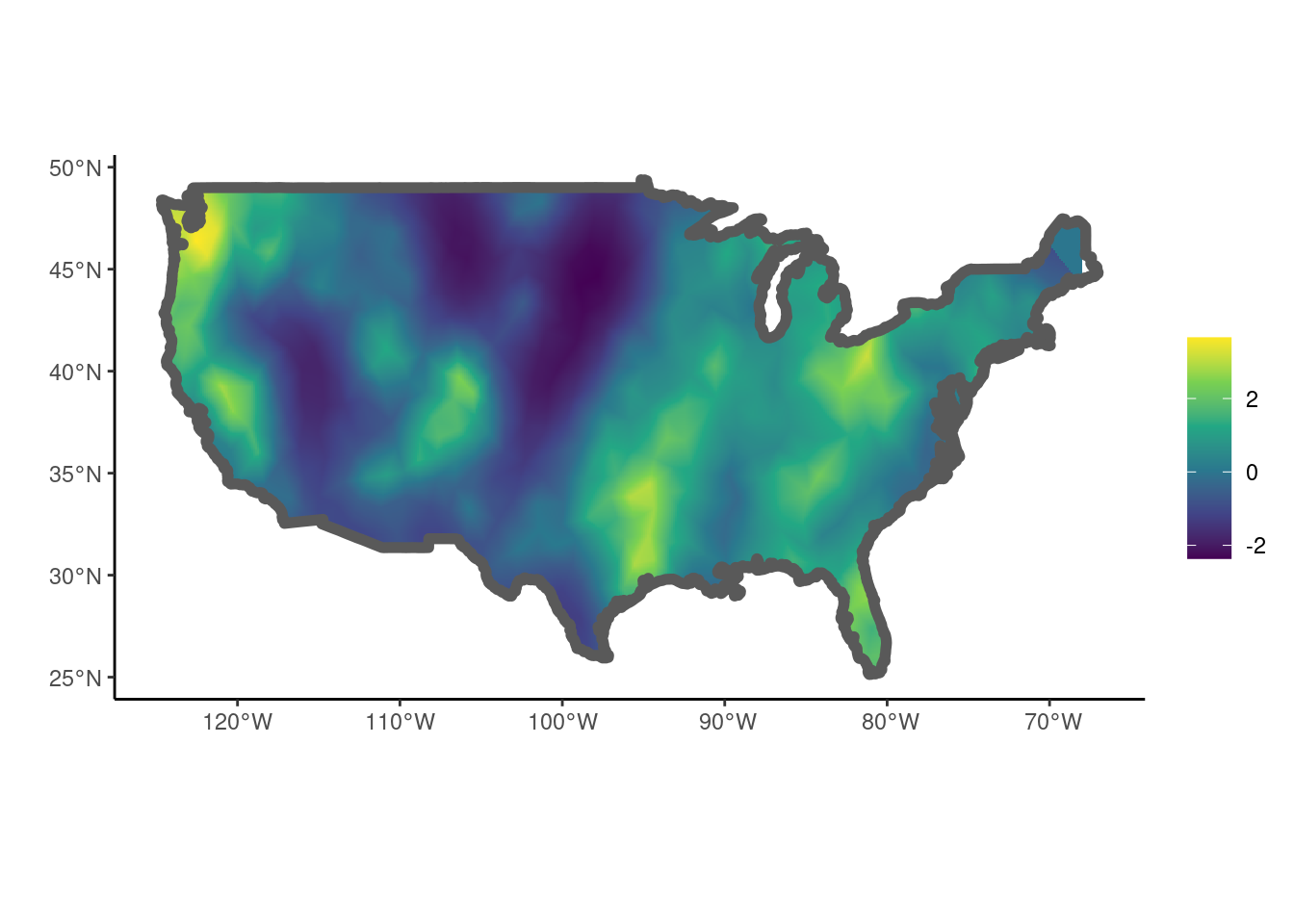
Fitting a model using stelfi
## dataframe of point locations
locs <- data.frame(x = sim$x, y = sim$y)
## Delauney triangulation of domain
smesh <- fmesher::fm_mesh_2d(loc = locs[, 1:2], max.edge = 0.2, cutoff = 0.1)
## sf of domain
sf <- sf::st_as_sf(win)
fit <- fit_lgcp(locs = locs, sf = sf, smesh = smesh,
parameters = c(beta = 3, log_tau = log(1),
log_kappa = log(1)))
get_coefs(fit) Estimate Std. Error
beta 3.2180075 0.2678925
log_tau -1.9447694 0.7069575
log_kappa 1.3917981 0.5967719
range 0.7032258 0.4196654
stdev 0.4903966 0.1469378The estimated GMRF can be plotted using the show_field() function once the values have been extracted using get_fields().
get_fields(fit, smesh) |>
show_field(smesh = smesh, sf = sf, clip = TRUE) + theme_void() +
geom_point(data = data.frame(x = sim$x, y = sim$y), aes(x = x, y = y))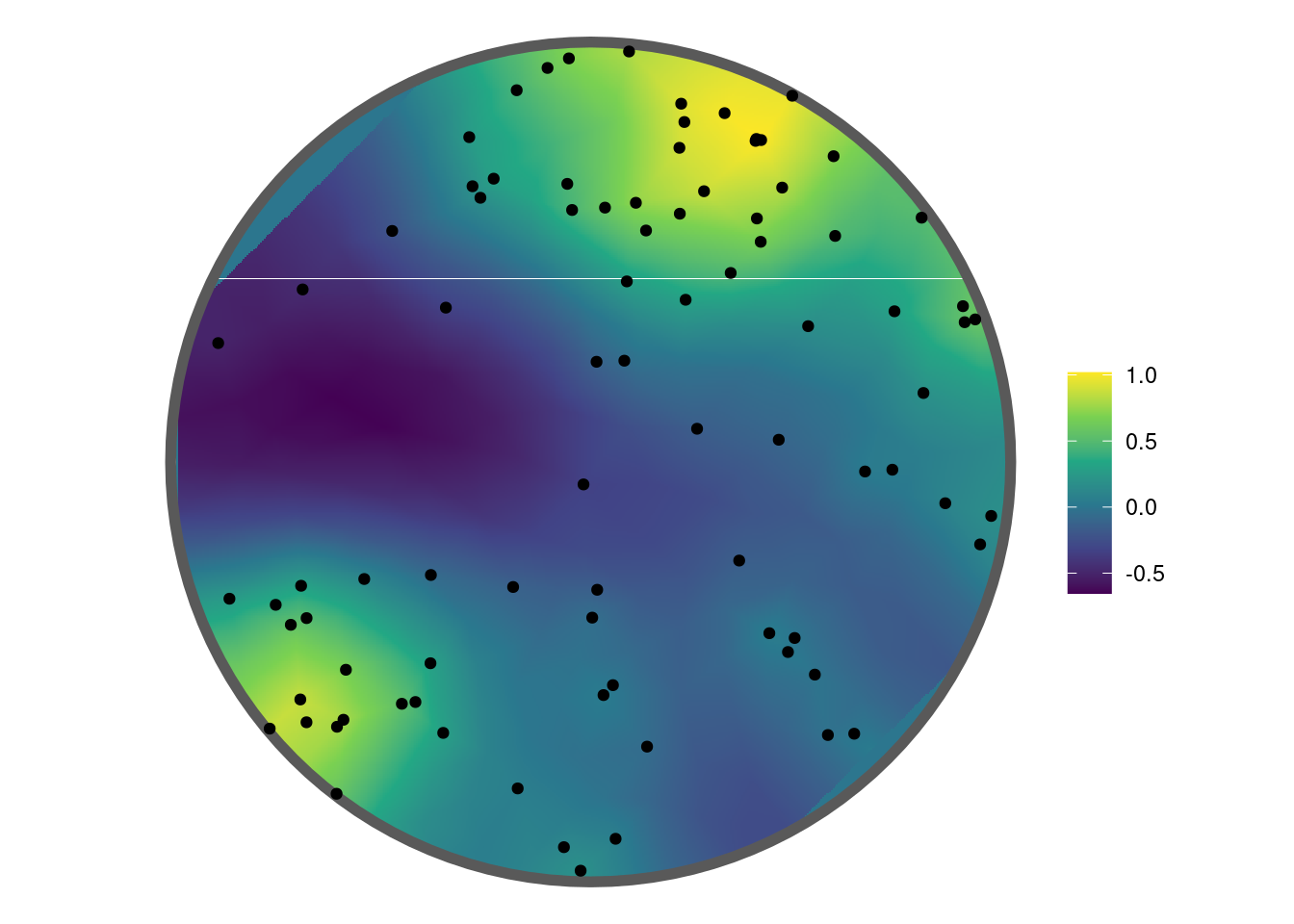
As a comparison, inlabru (Bachl et al. (2019)) is used to fit the same model to these data.
require(inlabru)
sf_locs <- sf::st_as_sf(locs, coords = c("x", "y"))
matern <- INLA::inla.spde2.pcmatern(smesh, prior.sigma = c(0.7, 0.01), prior.range = c(4, 0.5) )
## latent field
cmp <- geometry ~ random_field(geometry, model = matern) + Intercept(1)
## fit model
fit_inla <- lgcp(cmp, sf_locs, domain = list(geometry = smesh))
pars <- rbind(fit_inla$summary.fixed[,1:2], fit_inla$summary.hyperpar[,1:2])
parsNow using spatstat
ss <- spatstat.model::lgcp.estK(sim, covmodel = list(model = "matern", nu = 1))
ss$clustpar var scale
0.3541098 0.3018202 ss$modelpar sigma2 alpha mu
0.3541098 0.3018202 3.1445250 5.2.1 An applied example
Using the applied example given in Jones-Todd and van Helsdingen (2024) a LGCP model is fitted to sasquatch sightings using the function fit_lgcp(). For more details on the use of the Delauney triangulation see Section 5.1.
data("sasquatch", package = "stelfi")
## get sf of the contiguous US
sf::sf_use_s2(FALSE)
us <- maps::map("usa", fill = TRUE, plot = FALSE) |>
sf::st_as_sf() |>
sf::st_make_valid()
## dataframe of sighting locations (lat, long)
locs <- sf::st_coordinates(sasquatch) |>
as.data.frame()
names(locs) <- c("x", "y")
## Delauney triangulation of domain
smesh <- fmesher::fm_mesh_2d(loc = locs[, 1:2], max.edge = 2, cutoff = 1)
## fit model with user-chosen parameter starting values
fit <- fit_lgcp(locs = locs, sf = us, smesh = smesh,
parameters = c(beta = 0, log_tau = log(1),
log_kappa = log(1)))
get_coefs(fit) Estimate Std. Error
beta -0.7659374 0.3558810
log_tau -0.6109840 0.1028264
log_kappa -0.9540269 0.1510160
range 7.3430015 1.1089108
stdev 1.3491825 0.1480772Again, the estimated GMRF can be plotted using the show_field() function once the values have been extracted using get_fields().
get_fields(fit, smesh) |>
show_field(smesh = smesh, sf = us, clip = TRUE) + ggplot2::theme_classic()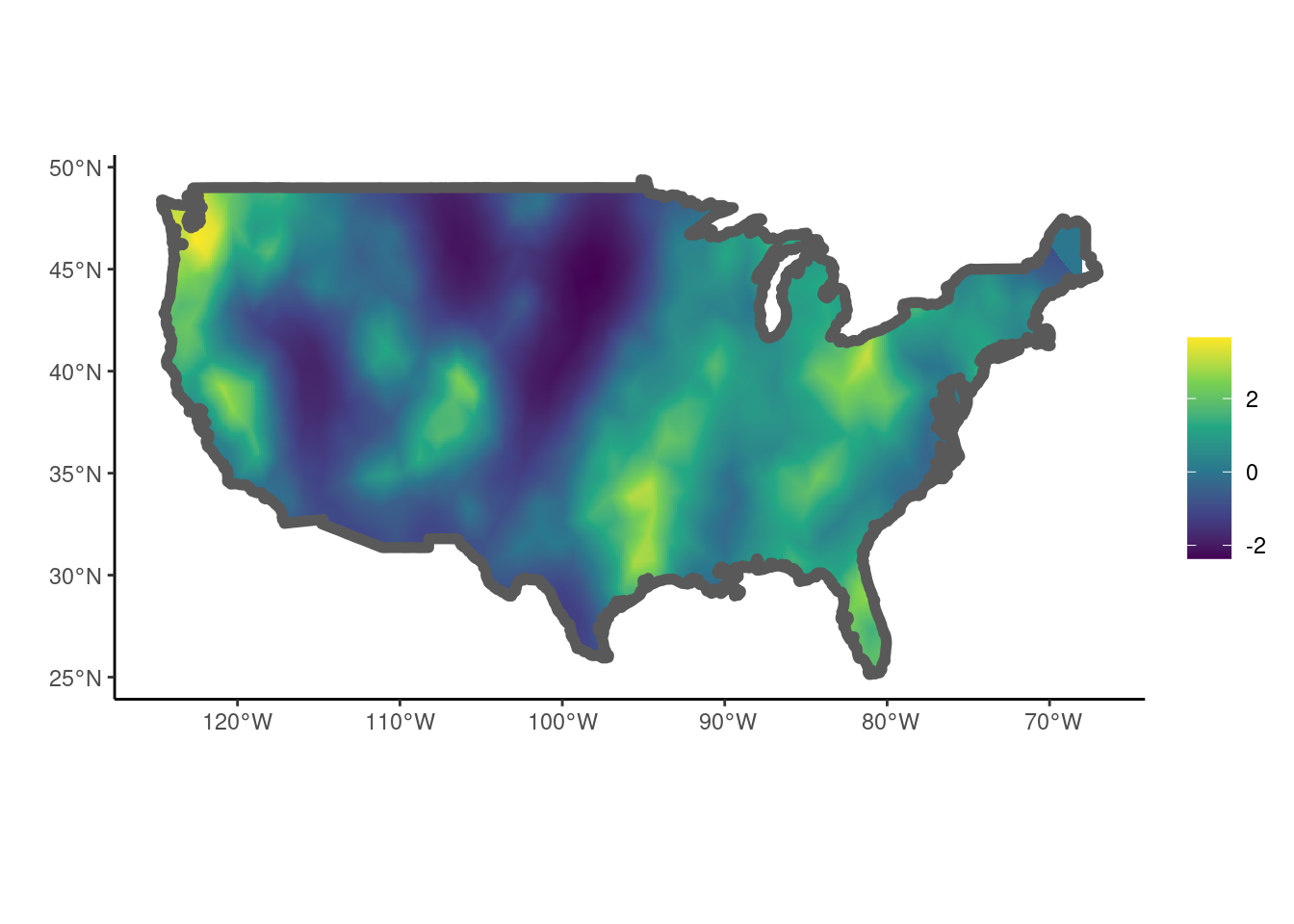
The estimated intensity surface can be plotted using the show_lambda() function.
show_lambda(fit, smesh = smesh, sf = us, clip = TRUE) + ggplot2::theme_classic()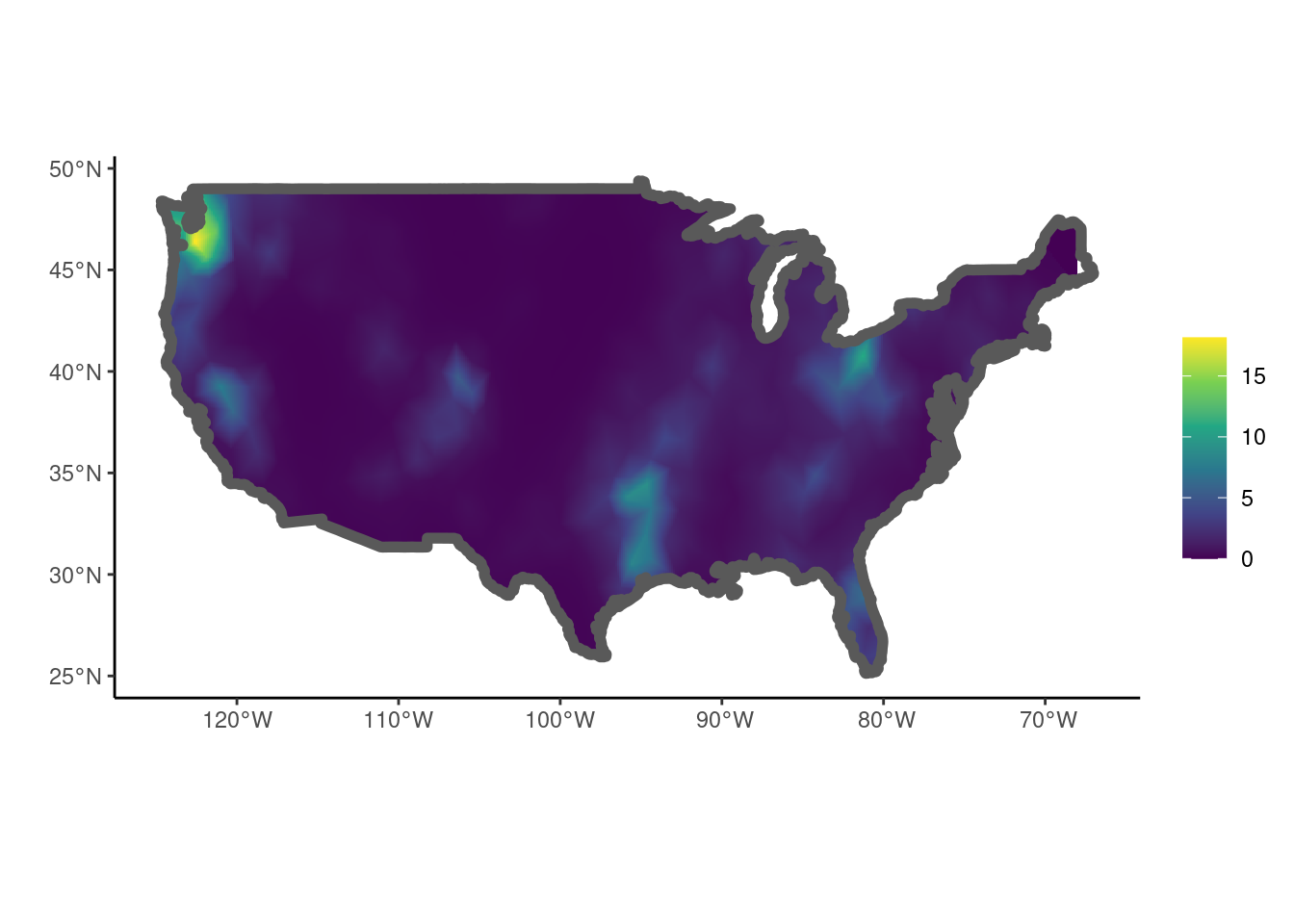
## Again, as a comparison, `inlabru` (@inlabru) is used to fit the same model to these data.
require(inlabru)
require(sp)
locs_sp <- locs; sp::coordinates(locs_sp) <- c("x", "y")
domain <- as(us, "Spatial")
matern <- INLA::inla.spde2.pcmatern(smesh,
prior.sigma = c(0.1, 0.01),
prior.range = c(5, 0.01)
)
## latent field
cmp <- coordinates ~ random_field(coordinates, model = matern) + Intercept(1)
sp::proj4string(locs_sp) <- smesh$crs <- sp::proj4string(domain)
## fit model
fit_inla <- lgcp(cmp, locs_sp, samplers = domain, domain = list(coordinates = smesh))
pars <- rbind(fit_inla$summary.fixed[,1:2], fit_inla$summary.hyperpar[,1:2])
pars5.3 SPDE as GAM
TODO