Chapter 3 Hawkes process

A univariate Hawkes process is defined to be a self-exciting temporal point process where the conditional intensity function is given by

\[\lambda(t) = \mu(t) + \Sigma_{i:\tau_i<t}\nu(t-\tau_i)\] where where \(\mu(t)\) is the background rate of the process and \(\Sigma_{i:\tau_i<t}\nu(t-\tau_i)\) is some historic temporal dependence. First introduced by Hawkes (1971), the classic homogeneous formulation is:

\[\lambda(t) = \mu + \alpha \Sigma_{i:\tau_i<t}\text{exp}(-\beta * (t-\tau_i)) \]

3.1 The fit_hawkes() function

## function (times, parameters = list(), model = 1, marks = c(rep(1, 
##     length(times))), tmb_silent = TRUE, optim_silent = TRUE, 
##     ...) 
## NULL

3.1.1 Fitting a Hawkes model

A NIWA scientist found a working USB in the scat of a leopard seal, they then tweeted about it in the hopes of finding its owner.

## [1] "2019-02-07 06:50:08 UTC" "2019-02-07 06:50:08 UTC"
## [3] "2019-02-07 06:49:22 UTC" "2019-02-07 06:48:48 UTC"
## [5] "2019-02-07 06:47:52 UTC" "2019-02-07 06:47:42 UTC"
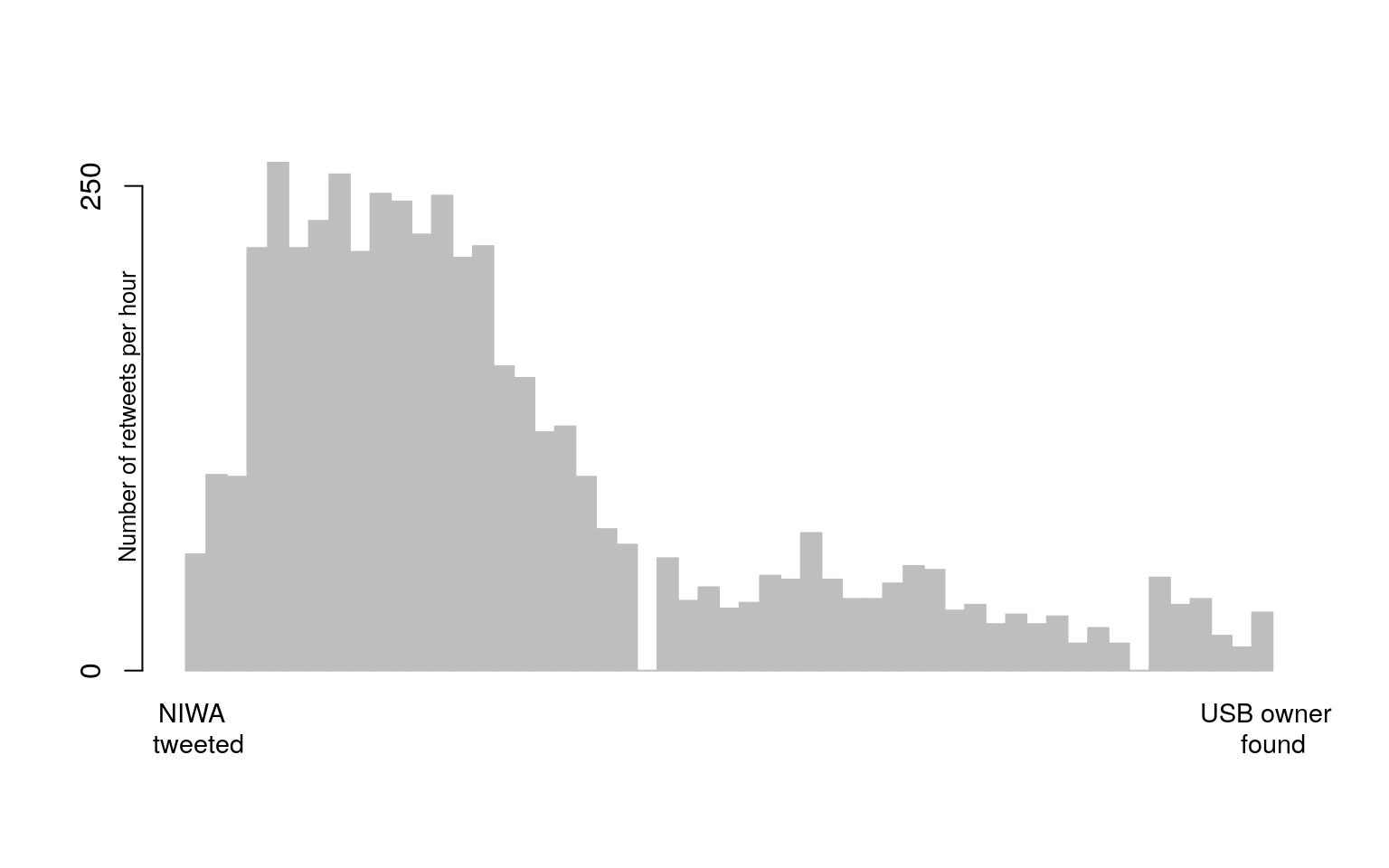
Observed counts of retweet times

(#fig:plot hist)Observed counts of retweet times 

##         Estimate  Std. Error
## mu    0.06328099 0.017783908
## alpha 0.07596531 0.007777899
## beta  0.07911346 0.008109789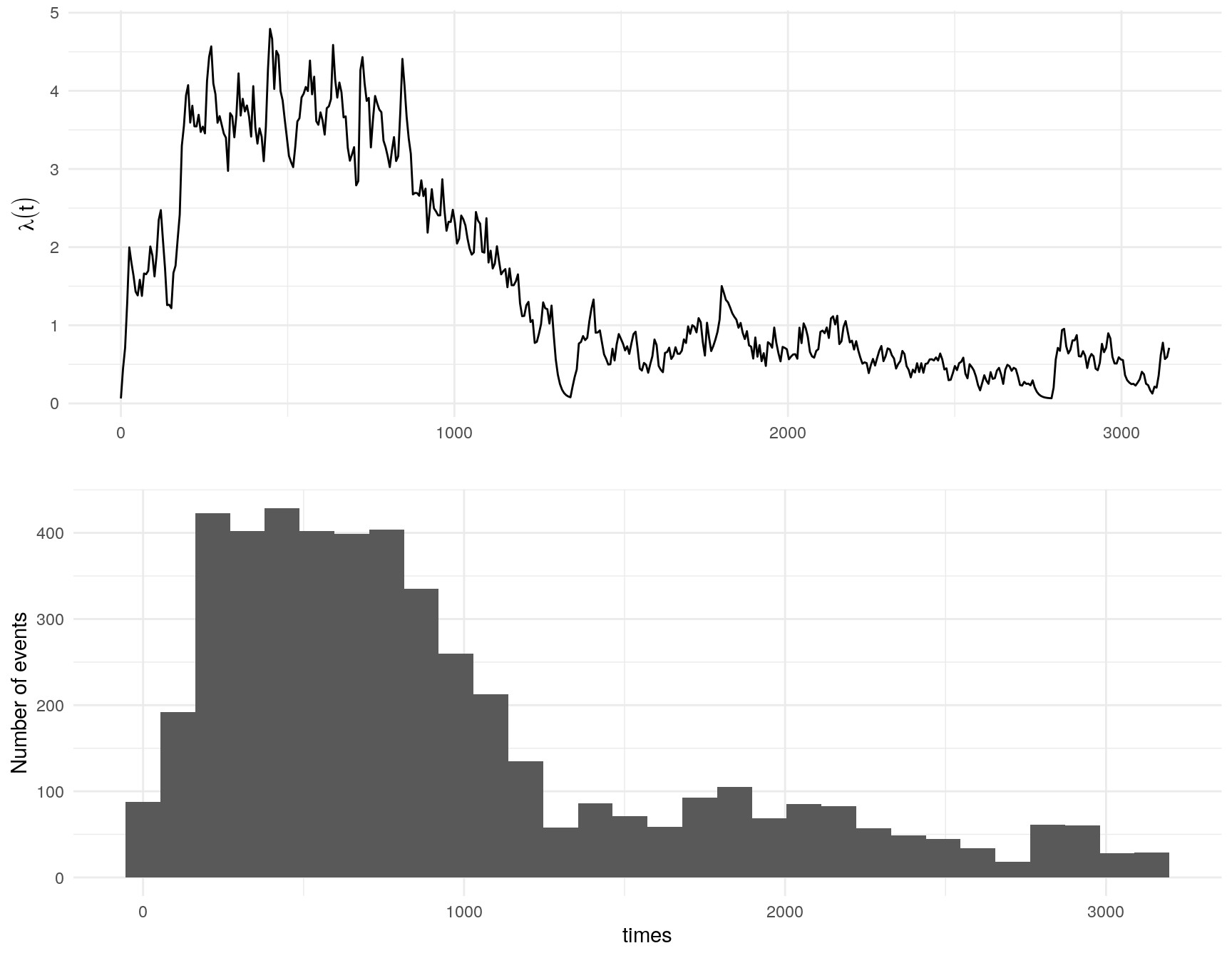

## 
##  Asymptotic one-sample Kolmogorov-Smirnov test
## 
## data:  interarrivals
## D = 0.031122, p-value = 0.0001937
## alternative hypothesis: two-sided
## 
## 
##  Box-Ljung test
## 
## data:  interarrivals
## X-squared = 3.3923, df = 1, p-value = 0.0655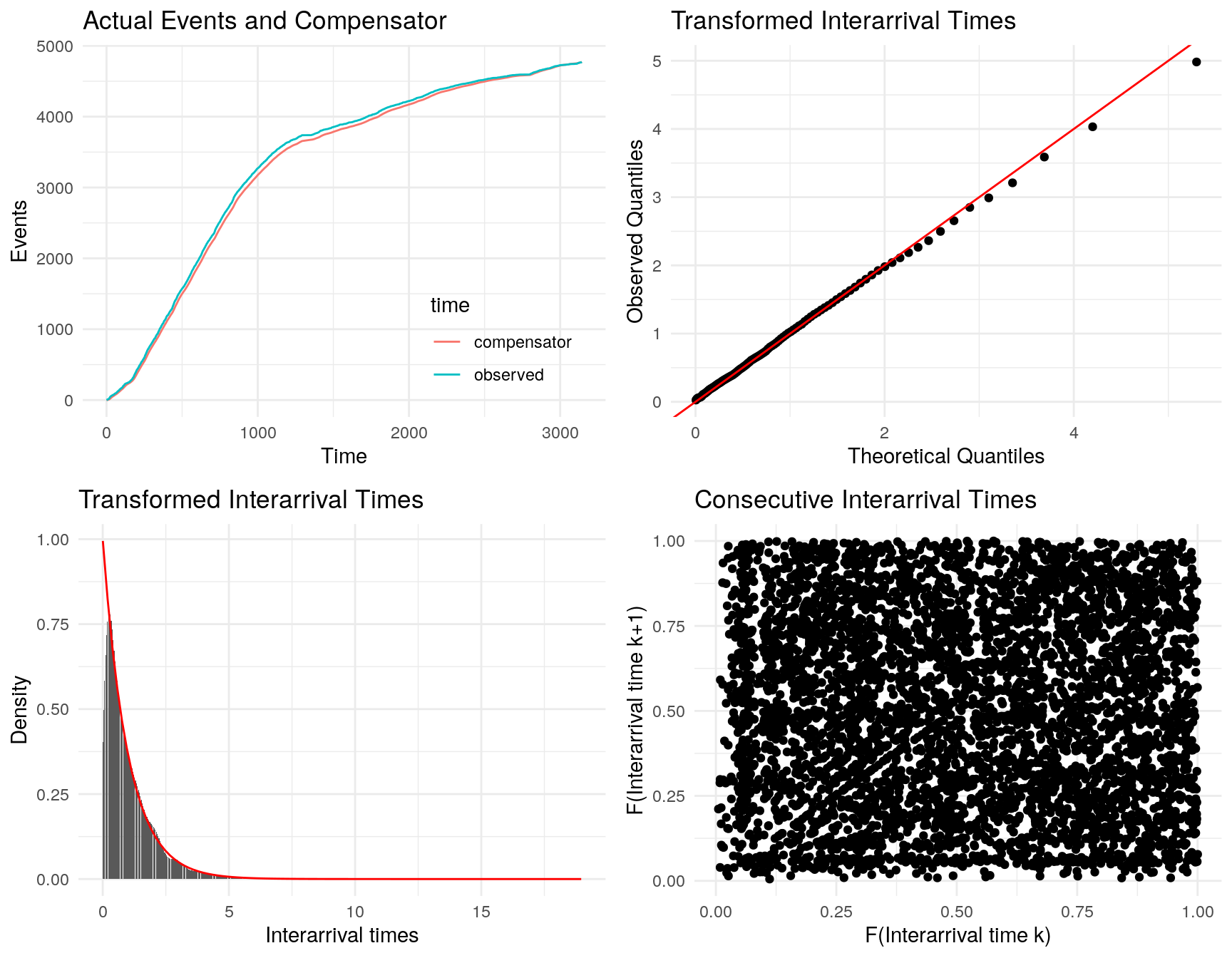

3.1.2 Fitting an ETAS-type marked model

Here we fit a univariate marked Hawkes process where the conditional intensity function is given by

\[\lambda(t; m(t)) = \mu + \alpha \Sigma_{i:\tau_i<t}m(\tau_i)\text{exp}(-\beta * (t-\tau_i)) \] where \(\mu\) is the background rate of the process and \(m(t)\) is the temporal mark. Each event \(i\) has an associated mark \(\tau_i\) that multiples the self-exciting component of \(\lambda\).

In this example, the events are earthquakes and the marks are the Richter magnitude of each earthquake.

## Simple feature collection with 6 features and 3 fields
## Geometry type: POINT
## Dimension:     XY
## Bounding box:  xmin: 172.3641 ymin: -43.63492 xmax: 172.7936 ymax: -43.42493
## CRS:           +proj=longlat +datum=WGS84 +no_defs +ellps=WGS84 +towgs84=0,0,0
##            origintime magnitude     depth                   geometry
## 1 2014-12-24 07:46:00  3.208996 13.671875 POINT (172.7133 -43.57944)
## 2 2014-12-24 06:43:00  4.109075  5.820312 POINT (172.7204 -43.55752)
## 3 2014-12-14 08:53:00  3.240377  5.058594 POINT (172.3641 -43.62563)
## 4 2014-12-12 13:37:00  4.459034  9.394531  POINT (172.368 -43.63492)
## 5 2014-11-20 08:24:00  3.116447 10.039062 POINT (172.7836 -43.42493)
## 6 2014-11-18 14:19:00  3.158710 11.269531  POINT (172.7936 -43.4897)
##           Estimate   Std. Error
## mu    0.0002001766 1.206014e-05
## alpha 0.0005125373 2.934243e-05
## beta  0.0020558328 1.204552e-04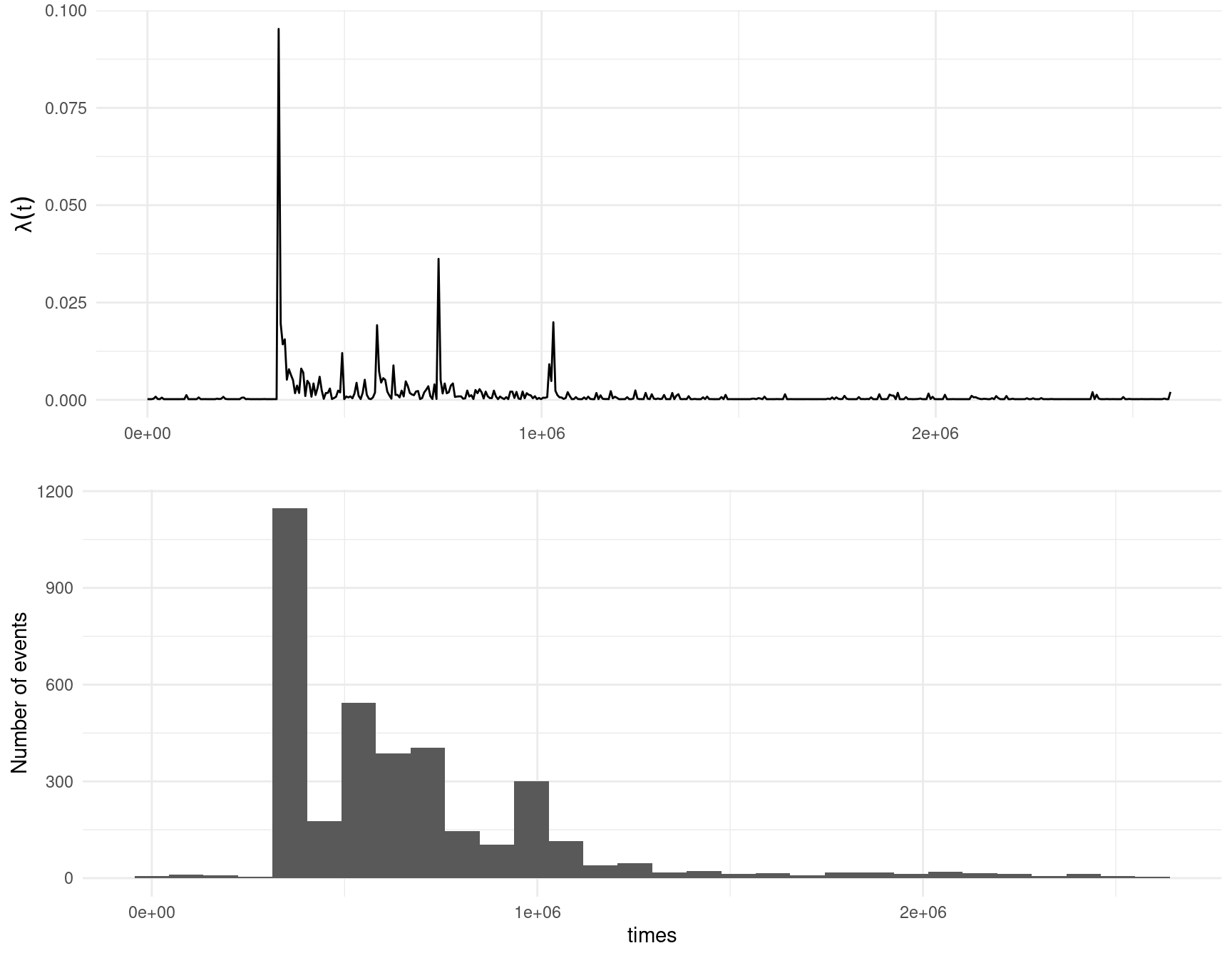

## 
##  Asymptotic one-sample Kolmogorov-Smirnov test
## 
## data:  interarrivals
## D = 0.035665, p-value = 0.0001912
## alternative hypothesis: two-sided
## 
## 
##  Box-Ljung test
## 
## data:  interarrivals
## X-squared = 104.09, df = 1, p-value < 2.2e-16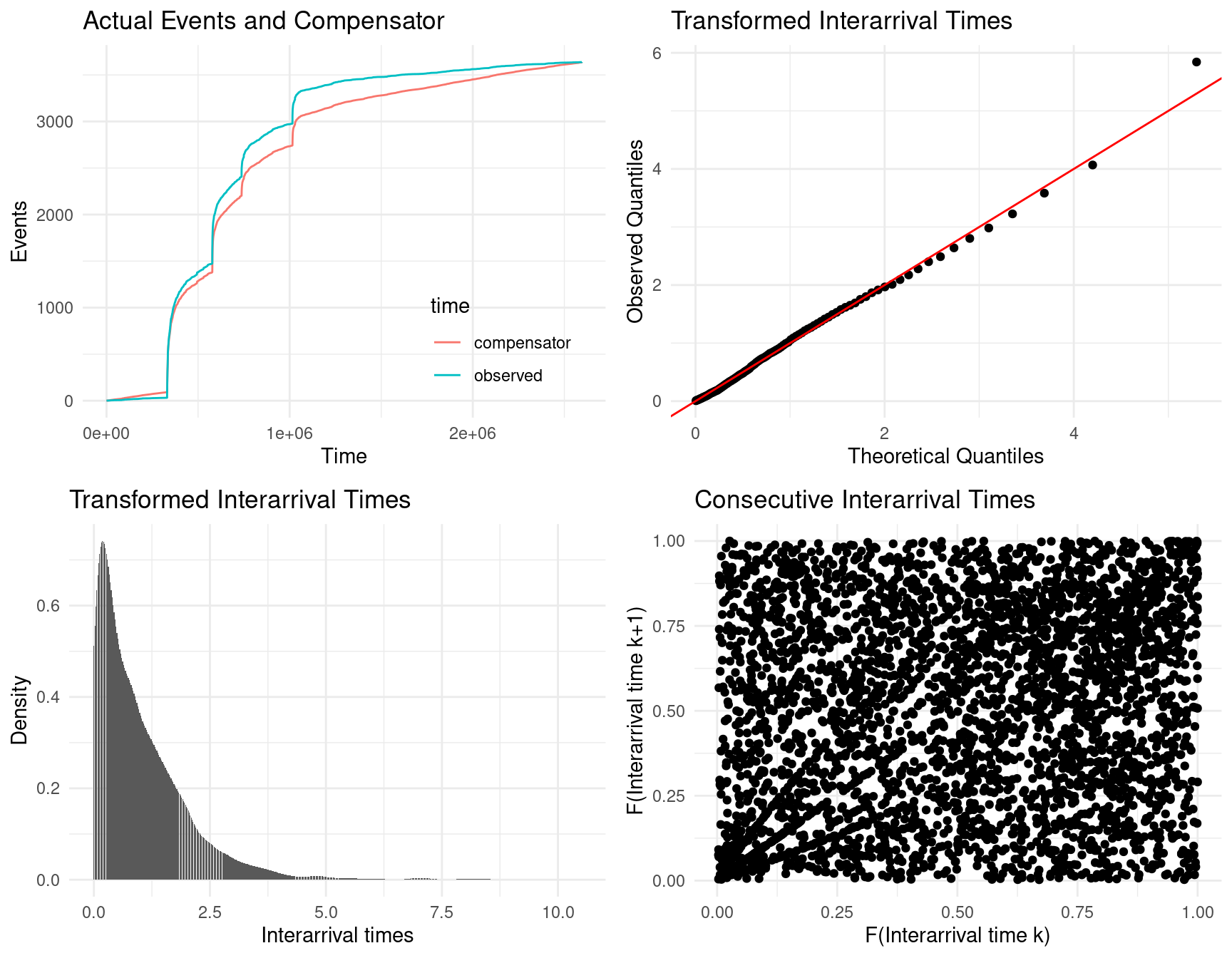

3.2 The fit_mhawkes() function

## function (times, stream, parameters = list(), tmb_silent = TRUE, 
##     optim_silent = TRUE, ...) 
## NULL

A multivariate Hawkes process allows for between- and within-stream self-excitement. In stelfi the conditional intensity for the \(j^{th}\) (\(j = 1, ..., N\)) stream is given by

\[\lambda(t)^{j*} = \mu_j + \Sigma_{k = 1}^N\Sigma_{i:\tau_i<t} \alpha_{jk} e^{(-\beta_j * (t-\tau_i))},\] where \(j, k \in (1, ..., N)\). Here, \(\alpha_{jk}\) is the excitement caused by the \(k^{th}\) stream on the \(j^{th}\). Therefore, \(\boldsymbol{\alpha}\) is an \(N \times N\) matrix where the diagonals represent the within-stream excitement and the off-diagonals represent the excitement between streams.

##        Estimate Std. Error
## mu    0.2767272 0.10705381
## mu    0.1891731 0.08795223
## alpha 0.5116696 0.19277471
## alpha 0.1260672 0.10338890
## alpha 0.1311323 0.08845832
## alpha 0.6173171 0.21126133
## beta  0.9492155 0.35596511
## beta  0.8316319 0.29757181

3.3 The fit_hawkes_cbf() function

## function (times, parameters = list(), model = 1, marks = c(rep(1, 
##     length(times))), background, background_integral, background_parameters, 
##     background_min, tmb_silent = TRUE, optim_silent = TRUE) 
## NULL

3.3.1 Fitting an inhomogenous Hawkes process

Here we fit a univariate inhomogenous marked Hawkes process where the conditional intensity function is given by

\[\lambda(t) = \mu(t) + \alpha \Sigma_{i:\tau_i<t}\text{exp}(-\beta * (t-\tau_i)) \] The background \(\mu(t)\) is time varying, rather than being constant.

The following example uses simulated data.

We will attempt to recover these parameter values, modelling the background as $ (t) = A + Bsin(t)$. The background will be written as a function of \(x\) and \(y\), where \(A = e^x\) and \(B= logit(y) e^x\). This formulation ensures the background is never negative.

The estimated values of \(A\) and \(B\) respectively are

## [1] 1.025526
## [1] 0.5635566

The estimated values of \(\alpha\) and \(\beta\) respectively are:

##    alpha     beta 
## 1.040863 2.179564

3.4 The sim_hawkes() function

## function (mu, alpha, beta, n = 100, plot = FALSE, seed = 123, 
##     method = "1") 
## NULL

method = 1

## [1] 0.6231314 0.7420664 0.7986166 2.0856174 2.1293941 2.4093639

method = 2

## [1] 0.6231314 0.7314123 1.1083232 1.1571593 1.1795519 2.2830958

References

Hawkes, AG. 1971. “Spectra of Some Self-Exciting and Mutually Exciting Point Processes.” Biometrika.