Chapter 5 Marked log-Gaussian Cox process
Each event in a spatial LGCP may have a scalar or vector mark associated with it. In that case, we are interested not only in the spatial intensity of the point process but also the spatial distribution of the marks and the correlation between the marks and the point process.
The intensity of the LGCP is as in the simple case: \[\Lambda_{pp}(s) = \text{exp}(\beta_{pp} + G_{pp}(s) + \epsilon)\] note the subscripts \(pp\) indicating the point process.
The mark(s) have their own field: \[\Lambda_m(s)=\beta_{m}+G_m(s)+\alpha \text{log}(\Lambda_{pp}(s)) +\epsilon\] where \(\alpha\) are coefficient(s) linking the point process and the mark(s). The meaning of \(\Lambda_m(s)\) depends on the distribution of the marks. If the marks are from a Poisson distribution, it is the intensity (as with the point process). If the marks are from a Binomial distribution, it is the success probability, and the user must supply the number of trials for each event. If the marks are normally distributed, \(\Lambda_m(s)\) models the mean, and the user must supply the standard deviation. The user can choose for the point processes and the marks to share a common GMRF, i.e. \(G_m(s) = G_{pp}(s)\)
5.1 The fit_mlgcp() function
## function (locs, sf, marks, smesh, parameters = list(), methods,
## strfixed = matrix(1, nrow = nrow(locs), ncol = ncol(marks)),
## fields = rep(1, ncol(marks)), covariates, pp_covariates,
## marks_covariates, tmb_silent = TRUE, nlminb_silent = TRUE,
## ...)
## NULL5.1.1 Fitting a marked LGCP
data(marked, package = "stelfi")
loc.d <- 3 * cbind(c(0, 1, 1, 0, 0), c(0, 0, 1, 1, 0))
domain <- sf::st_sf(geometry = sf::st_sfc(sf::st_polygon(list(loc.d))))
smesh <- INLA::inla.mesh.2d(loc.domain = loc.d, offset = c(0.3, 1),
max.edge = c(0.3, 0.7), cutoff = 0.05)
locs <- cbind(x = marked$x, y = marked$y)
marks <- cbind(m1 = marked$m1) ## Gaussian
parameters <- list(betamarks = matrix(0, nrow = 1, ncol = ncol(marks)),
log_tau = log(1), log_kappa = log(1),
marks_coefs_pp = rep(0, ncol(marks)), betapp = 0)
fit <- fit_mlgcp(locs = locs, marks = marks,
sf = domain, smesh = smesh,
parameters = parameters, methods = 0,
fields = 0)
get_coefs(fit)## Estimate Std. Error
## betamarks 9.9001308 0.3032841
## betapp 2.7353453 0.1310755
## marks_coefs_pp -0.2793250 0.4280345
## tau 0.1028983 0.0594815
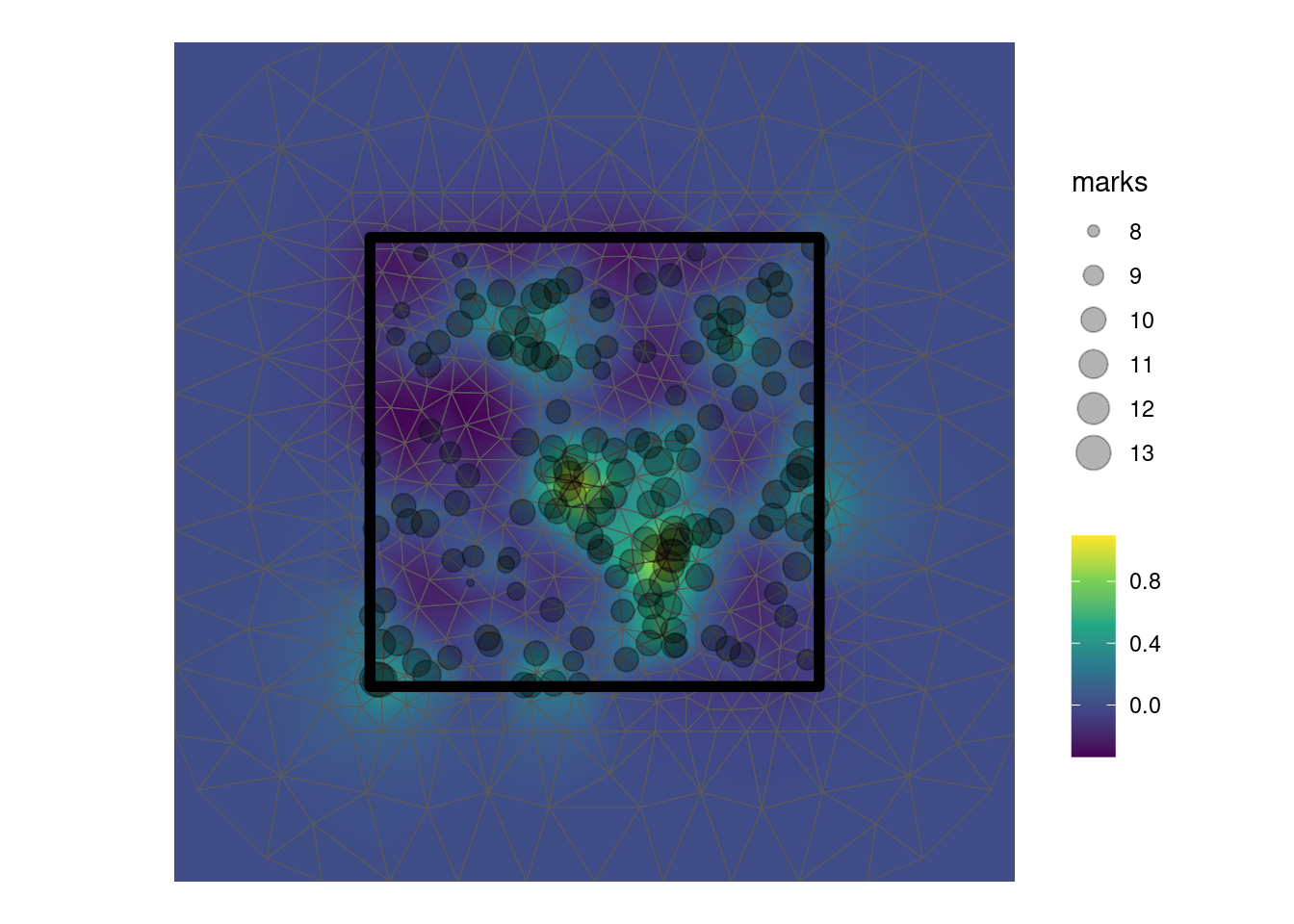
## kappa 5.8998690 2.6928689get_fields(fit, smesh) |>
show_field(smesh = smesh) +
geom_sf(data = mesh_2_sf(smesh), fill = NA) +
geom_sf(data = domain, fill = NA, col = "black", lwd = 2) +
geom_point(data = as.data.frame(locs), aes(x = x, y = y, cex = marks), alpha = 0.3, inherit.aes = FALSE) +
theme_void()